Dijkstra's Algorithm

此演算法是由一位叫 Edsger Dijkstra 的荷蘭工程師所發明，他在電腦科學領域貢獻了許多奠定目前網際網路、電腦科學與數位服務等等的基礎。

在學習 Dijkstra's Algorithm 需前理解資料結構的 Priority Queue 與 Graph 。

而 Dijkstra's Algorithm 正是用他的名字來命名，此演算法是用於找出在 Graph 中兩個節點之間的最短路徑。

由於找最短路徑的應用場景中，每兩個節點之間的距離可能都會不一樣，所以我們需要先實作一個 Weighted Graph 。

Weighted Graph

class WeightedGraph {
  constructor() {
    this.adjacencyList = {}
  }
  addVertex(vertex) {
    if (!this.adjacencyList[vertex]) this.adjacencyList[vertex] = []
  }
  addEdge(vertex1, vertex2, weight) {
    if (this.adjacencyList[vertex1] && this.adjacencyList[vertex2]) {
      this.adjacencyList[vertex1].push({node: vertex2, weight})
      this.adjacencyList[vertex2].push({node: vertex1, weight})
    }
  }
}

剩餘的部分可參考 Graph 章節。

Pseudo Code

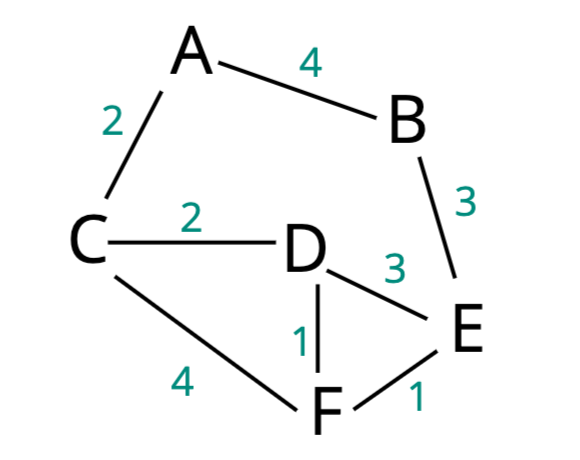
graph-ud-u

以上圖為例子，找尋從 A 到 E 的最短距離。

我們需要定義幾個變數：

distances - 記錄從初始節點到各個節點所需的距離
previous - 紀錄到各個節點時，上個節點是哪個

一開始初始化變數時，我們將 distances 的 A 節點紀錄為 0 (從 A 到 A 的距離當然為零)，其他的節點紀錄為 Infinity。 previous 則是各個節點都先設 null 。

設 Infinity 是為了等等在比大小取最短距離時，第一次給的值都能更新上去。

大概會像是這樣：

const distances = {
  A: 0,
  B: Infinity,
  C: Infinity,
  D: Infinity,
  E: Infinity,
  F: Infinity,
}
const previous = {
  A: null,
  B: null,
  C: null,
  D: null,
  E: null,
  F: null,
}

接著就開始第一步，從 distances 中找出目前距離初始節點 A 最短距離的節點：是 A ，因為其他預設值都是設 Infinity。

找出目前距離初起節點最短的 A 之後，將 A 相連的節點們一個個加上 A 紀錄的距離與 A 到該相鄰節點的距離，若此次計算出的距離比原本 distances 所紀錄的距離還短，我們就更新在 distances 上，並且 previous 也要紀錄這些相鄰節點的上個節點是 A ：

const distances = {
  A: 0,
  B: 4,
  C: 2,
  D: Infinity,
  E: Infinity,
  F: Infinity,
}
const previous = {
  A: null,
  B: 'A',
  C: 'A',
  D: null,
  E: null,
  F: null,
}

A 已經訪問過了，接續同樣動作，從 distances 找出剩下節點中目前距離初始節點 A 最短距離的節點：是 C 。

C 的相鄰節點們一個個加上 C 紀錄的距離與跟 C 之間的距離，若此次計算出的距離比原本 distances 所紀錄的距離還短，我們就更新在 distances 上，並且 previous 也要紀錄這些相鄰節點的上個節點是 C ：

const distances = {
  A: 0,
  B: 4,
  C: 2,
  D: 4,
  E: Infinity,
  F: 6,
}
const previous = {
  A: null,
  B: 'A',
  C: 'A',
  D: 'C',
  E: null,
  F: 'C',
}

C 已經訪問過了，從 distances 找出剩下節點中目前距離初始節點 A 最短距離的節點：是 B 跟 D ，先後順序不重要，這邊先選 B 出來。

B 的相鄰節點們一個個加上 B 紀錄的距離與跟 B 之間的距離，若此次計算出的距離比原本 distances 所紀錄的距離還短，我們就更新在 distances 上，並且 previous 也要紀錄這些相鄰節點的上個節點是 B ：

const distances = {
  A: 0,
  B: 4,
  C: 2,
  D: 4,
  E: 7,
  F: 6,
}
const previous = {
  A: null,
  B: 'A',
  C: 'A',
  D: 'C',
  E: 'B',
  F: 'C',
}

B 已經訪問過了，從 distances 找出剩下節點中目前距離初始節點 A 最短距離的節點：是 D 。

D 的相鄰節點們一個個加上 D 紀錄的距離與跟 D 之間的距離，若此次計算出的距離比原本 distances 所紀錄的距離還短，我們就更新在 distances 上，並且 previous 也要紀錄這些相鄰節點的上個節點是 D ：

const distances = {
  A: 0,
  B: 4,
  C: 2,
  D: 4,
  E: 7,
  F: 5,
}
const previous = {
  A: null,
  B: 'A',
  C: 'A',
  D: 'C',
  E: 'B',
  F: 'D',
}

D 已經訪問過了，從 distances 找出剩下節點中目前距離初始節點 A 最短距離的節點：是 F 。

F 的相鄰節點們一個個加上 F 紀錄的距離與跟 F 之間的距離，若此次計算出的距離比原本 distances 所紀錄的距離還短，我們就更新在 distances 上，並且 previous 也要紀錄這些相鄰節點的上個節點是 F ：

const distances = {
  A: 0,
  B: 4,
  C: 2,
  D: 4,
  E: 6,
  F: 5,
}
const previous = {
  A: null,
  B: 'A',
  C: 'A',
  D: 'C',
  E: 'F',
  F: 'D',
}

F 已經訪問過了，從 distances 找出剩下節點中目前距離初始節點 A 最短距離的節點：是 E 。

E 就是我們的終點節點，所以迴圈到此結束，目前 E 所紀錄的距離就是從 A 到 E 所需的最短距離。

而路徑我們則可以用 previous 來幫助我們回朔： E -> F -> D -> C -> A 。

Priority Queue

而找尋當前哪個節點擁有最短路徑這部分可以使用 Priority Queue 來實作，每次加進去時，會依照其優先度調整順序，之後要找最短路徑時只要拿第一個就好了。

用此資料結構也能有效降低時間複雜度，若用陣列找尋最小值的話每次都需要遍歷整個陣列 - O(n) ， Priority Queue 則是在調整順序時只需 - O(log n) 。

class Node {
  constructor(val, priority) {
    this.val = val
    this.priority = priority
  }
}
class PriorityQueue {
  constructor() {
      this.values = []
  }
  enqueue(val, priority) {
    let newNode = new Node(val, priority)
    this.values.push(newNode)
    this.bubbleUp()
  }
  bubbleUp() {
    let idx = this.values.length - 1
    const element = this.values[idx]
    while (idx > 0) {
      let parentIdx = Math.floor((idx - 1)/2)
      let parent = this.values[parentIdx]
      if (element.priority >= parent.priority) break
      this.values[parentIdx] = element
      this.values[idx] = parent
      idx = parentIdx
    }
  }
  dequeue() {
    const min = this.values[0]
    const end = this.values.pop()
    if (this.values.length > 0) {
      this.values[0] = end
      this.sinkDown()
    }
    return min
  }
  sinkDown() {
    let idx = 0
    const length = this.values.length
    const element = this.values[0]
    while (true) {
      let leftChildIdx = 2 * idx + 1
      let rightChildIdx = 2 * idx + 2
      let leftChild,rightChild
      let swap = null

      if (leftChildIdx < length) {
        leftChild = this.values[leftChildIdx]
        if (leftChild.priority < element.priority) {
          swap = leftChildIdx
        }
      }
      if (rightChildIdx < length) {
        rightChild = this.values[rightChildIdx]
        if (
          (swap === null && rightChild.priority < element.priority) || 
          (swap !== null && rightChild.priority < leftChild.priority)
        ) {
          swap = rightChildIdx
        }
      }
      if (swap === null) break
      this.values[idx] = this.values[swap]
      this.values[swap] = element
      idx = swap
    }
  }
}

sinkDown 的部分和另篇 Priority Queue 裡實作的較不一樣，不同的做法但都可以達成目標。

Implement

dijkstra(start, finish) {
  const nodes = new PriorityQueue()
  const distances = {}
  const previous = {}
  let path = [] // to return at end
  let smallest
  // build up initial state
  for (let vertex in this.adjacencyList) {
    if (vertex === start) {
      distances[vertex] = 0
      nodes.enqueue(vertex, 0)
    } else {
      distances[vertex] = Infinity
      nodes.enqueue(vertex, Infinity)
    }
    previous[vertex] = null
  }
  // as long as there is something to visit
  while (nodes.values.length) {
    smallest = nodes.dequeue().val
    if (smallest === finish) {
      // BUILD UP PATH TO RETURN AT END
      while (previous[smallest]) {
        path.push(smallest)
        smallest = previous[smallest]
      }
      break
    } 
    if (smallest || distances[smallest] !== Infinity) {
      for (let neighbor in this.adjacencyList[smallest]) {
        // find neighboring node
        let nextNode = this.adjacencyList[smallest][neighbor]
        // calculate new distance to neighboring node
        let candidate = distances[smallest] + nextNode.weight
        let nextNeighbor = nextNode.node
        if (candidate < distances[nextNeighbor]) {
          // updating new smallest distance to neighbor
          distances[nextNeighbor] = candidate
          // updating previous - How we got to neighbor
          previous[nextNeighbor] = smallest
          // enqueue in priority queue with new priority
          nodes.enqueue(nextNeighbor, candidate)
        }
      }
    }
  }
  return path.concat(smallest).reverse()     
}

Weighted Graph​

Pseudo Code​

Priority Queue​

Implement​

Weighted Graph

Pseudo Code

Priority Queue

Implement