Graph

簡言之， Graph 就是很多個節點與節點之間的連線所組成的，與前幾篇提到的 Three 也算是 Graph 的一種， Graph 主要有以下幾點特色：

Graph 沒有特定的根節點
節點之間的連線可以有或沒有方向性
一個節點可以任意與多個節點連線
節點之間的連線可以有權重 (例如地圖上兩個景點間的連線距離)

Graph 是目前最廣泛應用的資料結構之一，在社群網路、地圖與路線演算法、推薦廣告等等都可以用到。

當提到 Graph 時有幾點名詞與用途也要介紹一下：

Vertex - 節點
Edge - 節點之間的連線
Undirected - 節點之間的連線沒有方向性 (雙向)
Directed - 節點之間的連線有方向性 (單向或雙向)
Weighted - 節點之間的連線有權重
Unweighted - 節點之間的連線沒有權重

在實作前先來介紹兩種存 Graph 資料的方式：

Adjacency Matrix (相鄰矩陣)
Adjacency List (相鄰列表)

Storing Graph - Adjacency Matrix

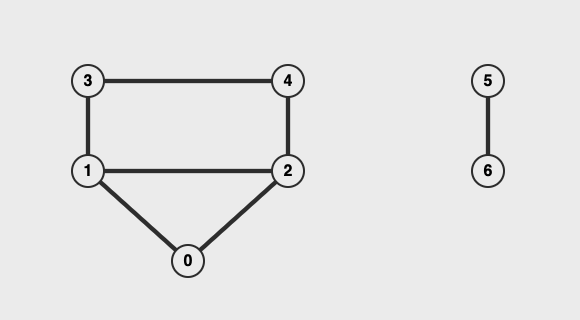
graph-uw-ud

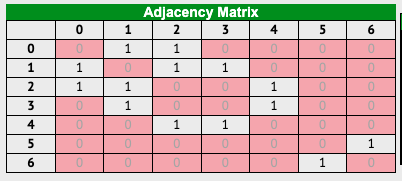
ad-matrix-uw-ud

來源

上圖範例為 Undirected 與 Unweighted 的 Graph ， Adjacency Matrix 以表格的方式來表示每個節點之間有無連線，有的話寫 1 、沒有的話寫 0 (要用 true 、 false 也可，只要能表示有無的就行)。

寫成程式碼會像這樣：

const adjacencyMatrix = [
  [0, 1, 1, 0, 0, 0, 0],
  [1, 0, 1, 1, 0, 0, 0],
  [1, 1, 0, 0, 1, 0, 0],
  [0, 1, 0, 0, 1, 0, 0],
  [0, 0, 1, 1, 0, 0, 0],
  [0, 0, 0, 0, 0, 0, 1],
  [0, 0, 0, 0, 0, 1, 0],
]

在程式上由於我們存的節點資料有可能是物件之類的資料，不會是像上面純數字，所以我們可以用其資料的 ID ，或是自己產個字串當作 Key 來存成物件形式。

//       Jason  Allan  Kevin  Alex  Vicky
// Jason   0      1      1      1     0
// Allan   1      0      1      0     0
// Kevin   1      1      0      0     0
// Alex    1      0      0      0     0
// Vicky   0      0      0      0     0

const adjacencyMatrix = {
  Jason: { Allan: true, Kevin: true, Alex: true, Vicky: false },
  Allan: { Jason: true, Kevin: true, Alex: false, Vicky: false },
  Kevin: { Jason: true, Allan: true, Alex: false, Vicky: false },
  Alex:  { Jason: true, Allan: false, Kevin: false, Vicky: false },
  Vicky: { Jason: false, Allan: false, Kevin: false, Alex: false },
}

Adjacency Matrix 重點在於就算某個節點沒有跟其他節點連線，也要存是否與其他節點連線的變數。

如 Vicky 都沒跟其他人有連線，但還是需要在自己的表格裡存有其他節點的名稱並標注 false 。

Storing Graph - Adjacency List

graph-uw-ud

ad-list-uw-ud

來源

上圖範例為 Undirected 與 Unweighted 的 Graph ， Adjacency List 以列表的方式來表示每個節點之間有無連線，有的話才會出現在列表內，反之則不在。

寫成程式碼會像這樣：

const adjacencyList = [
  [1, 2],
  [0, 2, 3],
  [0, 1, 4],
  [1, 4],
  [2, 3],
  [6],
  [5],
]

而用字串當 Key 存成物件形式的話則會像這樣：

const adjacencyList = {
  'Jason': [ 'Allan', 'Kevin', 'Alex' ],
  'Allan': [ 'Jason', 'Kevin' ],
  'Kevin': [ 'Jason', 'Allan' ],
  'Alex':  [ 'Jason' ],
  'Vicky': [],
}

Adjacency List 重點在於只存有關聯的節點，有關連的節點才會在該節點的關係列表中出現。

如 Vicky 都沒跟其他人有連線，所以他的列表就是空的。

Big O Complexity with Adjacency List & Matrix

|V| - 節點的數量 |E| - 連線的數量

Operation	Adjacency List	Adjacency Matrix
Add Vertex	`O(1)`	`O(
Add Edge	`O(1)`	`O(1)`
Remove Vertex	`O(	V
Remove Edge	`O(E)`	`O(1)`
Query	`O(	V
Storage	`O(	V

以下簡稱 List 與 Matrix

List 因為只存有連線關係的節點，所以比 Matrix 在記憶體使用上會較少。同個原因，所以 List 在遍歷所有連線時會比 Matrix 快。

但在查找特定連線時， Matrix 會比 List 快許多。

Implementation - Adjacency List Ver.

為何用 Adjacency List 呢？

因為在實際情況下，節點與節點之間並沒有那麼多的連線，就像社群網站 FB ，假設我有 1000 個好友，但 FB 總用戶至少也有好幾個億，若用 Adjacency Matrix 的話，我只有跟另外 1000 個節點有連線而已，剩下好幾個億節點也都要跟著存 0 條連線，這樣看起來 Adjacency List 是個比較好的選擇。

但一切依當下要解決的情境而定，也會有 Adjacency Matrix 適合的場景。

以下實作以字串當作 Key 來存節點的 Adjacency List 以及 Undirected, Unweighted 版本的 Graph ：

class Graph{
  constructor(){
    this.adjacencyList = {}
  }
}

Add & Remove Edge

addEdge(vertex1,vertex2){
  if (this.adjacencyList[vertex1] && this.adjacencyList[vertex2]) {
    this.adjacencyList[vertex1].push(vertex2);
    this.adjacencyList[vertex2].push(vertex1);
  }
}

removeEdge(vertex1,vertex2){
  this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
    v => v !== vertex2
  );
  this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
    v => v !== vertex1
  );
}

Add & Remove Vertex

Remove Vertex 時除了刪掉該節點之外，也要刪掉其他節點與此節點有連線的部分。

addVertex(vertex){
  if(!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
}

removeVertex(vertex){
  if(this.adjacencyList[vertex]) return
  while(this.adjacencyList[vertex].length){
    const adjacentVertex = this.adjacencyList[vertex].pop();
    this.removeEdge(vertex, adjacentVertex);
  }
  delete this.adjacencyList[vertex]
}

Storing Graph - Adjacency Matrix​

Storing Graph - Adjacency List​

Big O Complexity with Adjacency List & Matrix​

Implementation - Adjacency List Ver.​

Add & Remove Edge​

Add & Remove Vertex​